Consider the exponential function

$e^x = 1 + x + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + \frac{x^5}{120} + \cdots = \sum_{n=0}^\infty \frac{x^n}{n!}$

it is evident that if you evaluate $e^x$ at two arbitrary real numbers $x_0 < x_1$ that larger order terms in the taylor expansion are more important when you evaluate the the bigger term $e^{x_1}$ compared with the smaller term $e^{x_0}$, but how exactly does the weight of the importance shift with different values of $x$? I wanted to answer this question so I made this little gif, and the answer is surprisingly elegent: the dominant term of the taylor expansion is $e^k:k\in\mathbb N$ is $k$, and the distrubution looks pretty poissonian! You can certainly see a trend, where the standard deviation which I very crudly approximated looks like it's tending towards the square root of the number at which the series is being evaluated :).

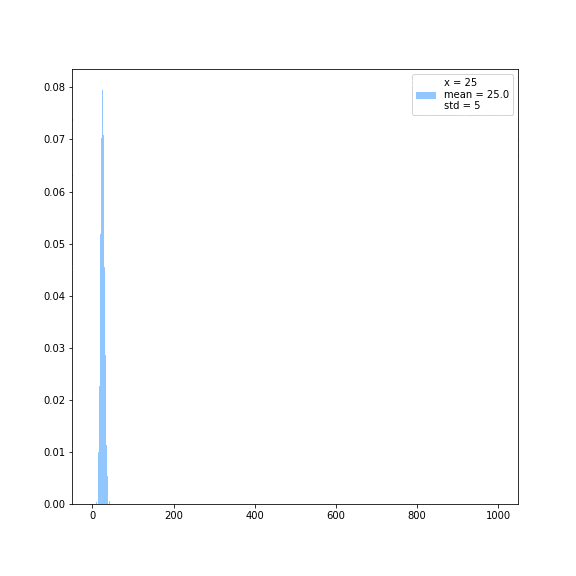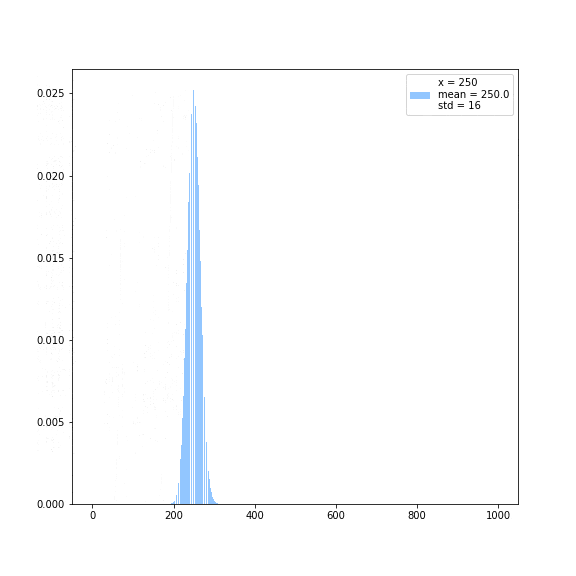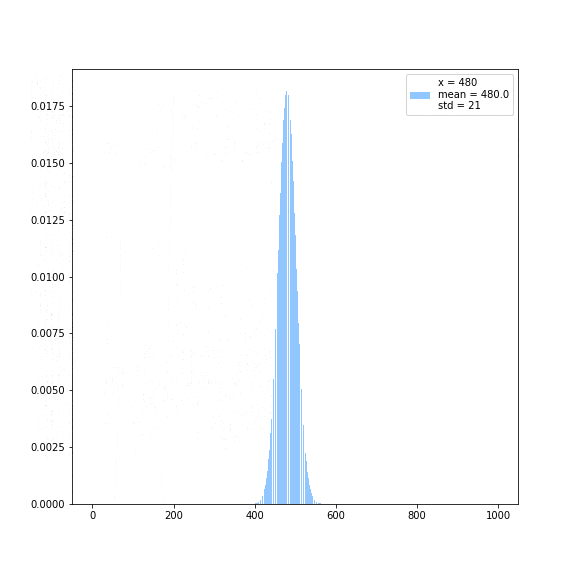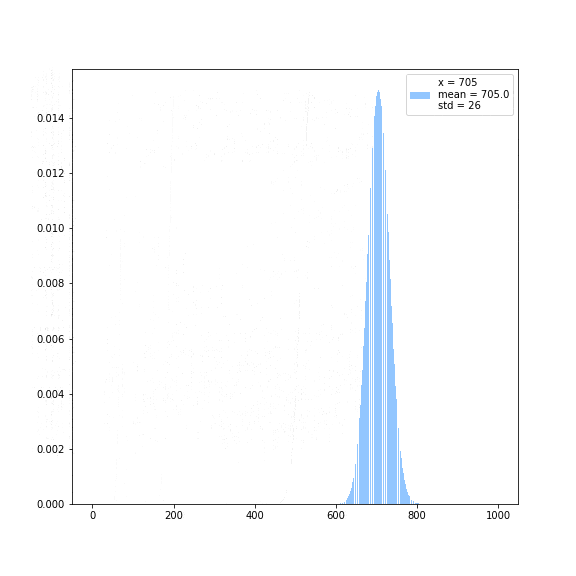
Denali says: This makes sense because if you fix $x$, then consider the ratio of the n plus one'th term and the n minus one'th term.

$\frac{x^{n+1}}{(n+1)!}\frac{n!}{x^n} = \frac{x}{n+1}$

the $n+1$ th term onle becomes more important than the $n$th term when $x > n+1$

You can find the above gif here, also if you'd like to see the source code it's in the same file in that repository.